Simple Pendulum

The Dutch astronomer Christiaan Huygens is credited with first suggesting the use of a pendulum in a clock to regulate its movement. Pendulums are useful because they have an extremely interesting property: The period (the amount of time it takes for a pendulum to go back and forth once) of a pendulum's swing is related only to the length of the pendulum and the force of gravity. Since gravity is constant at any given spot on the planet, the only thing that affects the period of a pendulum is the length of the pendulum. The amount of weight does not matter. Nor does the length of the arc that the pendulum swings through. Only the length of the pendulum matters.

The pendulum used in my wooden clocks is in technical terms a simple pendulum, in essence, a mass suspended from a fixed point so that it can swing back and forth under the influence of gravity.

Real  pendulums have the mass fixed to the end of the pendulum rod so the actual centre of the mass of the whole pendulum is, in reality, a little closer to the pivot as shown in the diagrams below because the rod itself has some mass.

The formulae for calculating the period of swing is -

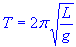
What is probably more useful is to work out the Length to the centre of mass so that we can set the initial length of the pendulum, to do that use-

 

where T = Period of oscillation, i.e. time to swing back and forth.
             L = Length from Pivot to the centre of mass.
             g = Acceleration due to Gravity meters/second^2   (9.81m/s^2)
             Pi (π) = 3.142

For most of my clocks I use a 2 seconds pendulum i.e. the time to swing back and forth is 2 seconds.

To work out the length of the pendulum from the pivot point to its centre of mass use above formula.
      

L=2²*9.81÷(4*3.142²) = 0.993 meters

For a 1 second pendulum used on Clocks 9,12 and 14

L=1²*9.81÷(4*3.142²) = 0.248meters

Links to Useful Websites:

Useful Formulae for Simple Pendulum calcs

http://www.ajdesigner.com/phppendulum/simple_pendulum_equation_period.php

History of the Pendulum use in clocks
http://en.wikipedia.org/wiki/Pendulum_clock#Atmospheric_drag